


Next: Efficiency factors
Up: Statistical Properties
Previous: Optimality criteria
Contents
In addition to the optimality criteria just listed, we also implement several
ordering criteria for block designs (optimality criteria are ordering criteria
that meet conditions described fully in a later subsection).
- no_distinct_canonical_variances
The number of distinct 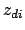 . For balanced incomplete block
designs this value is 1. A balance criterion; the fewer variances a
design produces, the easier are the results to understand.
. For balanced incomplete block
designs this value is 1. A balance criterion; the fewer variances a
design produces, the easier are the results to understand.
- max_min_ratio_canonical_variances
The ratio of largest to smallest canonical variance (
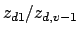 ), called the canonical variance ratio. Again, the
value for a balanced incomplete block design is 1. Values close to one
correspond to variances that are quite similar.
), called the canonical variance ratio. Again, the
value for a balanced incomplete block design is 1. Values close to one
correspond to variances that are quite similar.
- no_distinct_pairwise_variances
The number of distinct 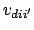 . Analogous to
no_distinct_canonical_variances, but for pairwise
variances rather than canonical variances.
. Analogous to
no_distinct_canonical_variances, but for pairwise
variances rather than canonical variances.
- element max_min_ratio_pairwise_variances
The ratio of largest to smallest pairwise variance (
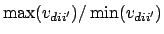 ), called the pairwise variance ratio. Analogous to
max_min_ratio_canonical_variances, but for pairwise
variances rather than canonical variances.
), called the pairwise variance ratio. Analogous to
max_min_ratio_canonical_variances, but for pairwise
variances rather than canonical variances.
- trace_of_square
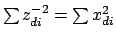 .
.
The trace of the square of 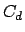 . This is called the S-criterion.
Typically invoked as part of an (M,S)-optimality argument (minimize S
subject to maximizing the trace of
. This is called the S-criterion.
Typically invoked as part of an (M,S)-optimality argument (minimize S
subject to maximizing the trace of 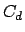 ). No direct statistical
interpretation, though usually leads to reasonably ``good'' designs.
). No direct statistical
interpretation, though usually leads to reasonably ``good'' designs.
It was mentioned above that a complete block design (each block size is
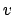 and each treatment is assigned to one unit in each block) is a
``good'' design. Now we state why. Over all possible assignments of
and each treatment is assigned to one unit in each block) is a
``good'' design. Now we state why. Over all possible assignments of 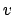 treatments to
treatments to 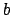 blocks of size
blocks of size 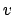 , a complete block design minimizes
all of the criteria defined above
(save for tr(
, a complete block design minimizes
all of the criteria defined above
(save for tr(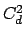 ), which it minimizes
subject to the mean of the unsquared components).
The same statement holds for a
balanced incomplete block design for constant block size less than
), which it minimizes
subject to the mean of the unsquared components).
The same statement holds for a
balanced incomplete block design for constant block size less than 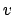 (whenever a BIBD exists). Otherwise, the optimal block design problem
can be quite tricky, with such uniform optimality hard to come by.
(whenever a BIBD exists). Otherwise, the optimal block design problem
can be quite tricky, with such uniform optimality hard to come by.
An optimality_value for any of the optimality
criteria above has three
elements: its numerical value and two associated numbers
absolute_efficiency and calculated_efficiency
(for other_ordering_criteria,
the same concepts are implemented under the names
absolute_comparison and calculated_comparison
so are not separately discussed here - see the
later subsection on design orderings).
Given any two designs, 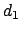 and
and 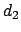 say, they can be compared on any of
the listed optimality criteria.
The relative efficiency of design
say, they can be compared on any of
the listed optimality criteria.
The relative efficiency of design 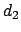 with
respect to criterion
with
respect to criterion 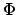 , compared to design
, compared to design 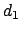 , is
, is
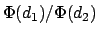 . If
. If 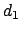 is in fact an optimal design as
measured by
is in fact an optimal design as
measured by 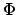 (
(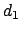 minimizes
minimizes 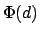 over all
over all 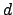 ), then the
relative efficiency of any
), then the
relative efficiency of any 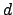 compared to
compared to 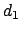 is the
absolute_efficiency of
is the
absolute_efficiency of 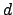 . Both of these efficiencies are between 0 and 1,
with smaller criterion values corresponding to larger efficiencies;
the absolute efficiency of an
optimal design is 1.
. Both of these efficiencies are between 0 and 1,
with smaller criterion values corresponding to larger efficiencies;
the absolute efficiency of an
optimal design is 1.
The concept of absolute efficiency
depends on what is meant by the phrase ``all 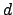 ''. It has already been
explained that comparisons are for designs with the same
''. It has already been
explained that comparisons are for designs with the same 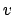 ,
, 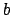 , and
block sizes. In the external representation, an
absolute_efficiency is for the class of all binary
designs with the same
, and
block sizes. In the external representation, an
absolute_efficiency is for the class of all binary
designs with the same 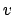 ,
, 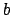 , and block size distribution, called the
reference universe. When the minimum criterion value over the
reference universe is not known, absolute_efficiency takes
the value ``unknown.'' For a disconnected design
absolute_efficiency takes the value ``0'' regardless of
whether the optimal value is known or not. It happens, only rarely, that
a smaller value of a criterion can be found for a nonbinary design with
the same
, and block size distribution, called the
reference universe. When the minimum criterion value over the
reference universe is not known, absolute_efficiency takes
the value ``unknown.'' For a disconnected design
absolute_efficiency takes the value ``0'' regardless of
whether the optimal value is known or not. It happens, only rarely, that
a smaller value of a criterion can be found for a nonbinary design with
the same 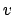 ,
, 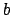 , and block sizes, in which case the
absolute_efficiency of the nonbinary design will be greater
than 1. Nonbinary designs are not at present considered in the external
representation. Relative efficiencies when the best value over the
reference universe is not known, or within a subclass of the reference
universe, can be calculated on a case-by-case basis; in external
representation terminology, this is a calculated_efficiency.
For instance, one may wish to compare only resolvable designs.
calculated_efficiency takes the value ``0'' for all
disconnected designs.
, and block sizes, in which case the
absolute_efficiency of the nonbinary design will be greater
than 1. Nonbinary designs are not at present considered in the external
representation. Relative efficiencies when the best value over the
reference universe is not known, or within a subclass of the reference
universe, can be calculated on a case-by-case basis; in external
representation terminology, this is a calculated_efficiency.
For instance, one may wish to compare only resolvable designs.
calculated_efficiency takes the value ``0'' for all
disconnected designs.



Next: Efficiency factors
Up: Statistical Properties
Previous: Optimality criteria
Contents
Peter Dobcsanyi
2003-12-15
![]() . For balanced incomplete block
designs this value is 1. A balance criterion; the fewer variances a
design produces, the easier are the results to understand.
. For balanced incomplete block
designs this value is 1. A balance criterion; the fewer variances a
design produces, the easier are the results to understand.
![]() ), called the canonical variance ratio. Again, the
value for a balanced incomplete block design is 1. Values close to one
correspond to variances that are quite similar.
), called the canonical variance ratio. Again, the
value for a balanced incomplete block design is 1. Values close to one
correspond to variances that are quite similar.
![]() . Analogous to
no_distinct_canonical_variances, but for pairwise
variances rather than canonical variances.
. Analogous to
no_distinct_canonical_variances, but for pairwise
variances rather than canonical variances.
![]() ), called the pairwise variance ratio. Analogous to
max_min_ratio_canonical_variances, but for pairwise
variances rather than canonical variances.
), called the pairwise variance ratio. Analogous to
max_min_ratio_canonical_variances, but for pairwise
variances rather than canonical variances.
![]() .
.
![]() . This is called the S-criterion.
Typically invoked as part of an (M,S)-optimality argument (minimize S
subject to maximizing the trace of
. This is called the S-criterion.
Typically invoked as part of an (M,S)-optimality argument (minimize S
subject to maximizing the trace of ![]() ). No direct statistical
interpretation, though usually leads to reasonably ``good'' designs.
). No direct statistical
interpretation, though usually leads to reasonably ``good'' designs.