The statistical properties of
fully developed hydrodynamic turbulence
can be well understood using techniques from
a generalized version of statistical mechanics,
so-called
nonextensive statistical mechanics
and superstatistics.
Look at my PRL (2007)
on Lagrangian turbulence, and more recent papers in
PRE and EPL on quantum turbulence
(the turbulent state of superfluid Helium).
The
stochastic models that are relevant for this are based on the so-called
superstatistics approach.
The following picture shows probability densities
of velocity differences as measured on
various scales in a
turbulent Taylor-Couette flow, and the theoretical predictions
of a model based on nonextensive statistical mechanics.
There is excellent agreement. Other theoretical
models for probability densities
in turbulent flows do not yield anything of similar precision.
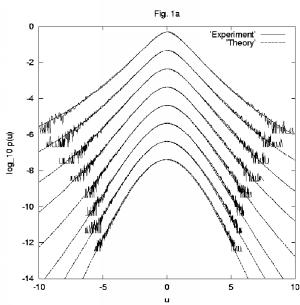
The measurements were made by Greg Lewis and Harry Swinney
at the
Center for Nonlinear Dynamics, University of Texas at Austin.
More details can be found in the following references:
C. Beck, G.S. Lewis, and H.L. Swinney,
Measuring non-extensitivity parameters in a turbulent Couette-Taylor
flow, Phys. Rev 63E ,
035303(R) (2001)
ps file available
C. Beck,
Dynamical foundations of nonextensive statistical mechanics,
Phys. Rev. Lett. 87 , 180601 (2001)
ps file available
Here is a link to a
popular science
article on my turbulence work.
An article in the SCIENCE magazin
(23 August 2002) also mentions this.
