A more modern interpretation is that this is an
effective description taking into account temperature fluctuations,
or generally the fluctuations of some variance parameter, the so-called
superstatistics approach.
The more general formalism is in particular useful for
the description of systems with long-range interactions,
multifractal behaviour, and fluctuations of temperature
or energy dissipation rate. Examples of
physical applications
are nonequilibrium
systems with a stationary state (including
turbulent flows), scattering
processes in elementary particle
physics,
and also applications for the dynamics of frequency fluctuations
in power grids,
as well as environmental time series such as
pollution concentrations.
Look at my most recent publications
on the subject in Nature Energy 2018 and Phys. Rev. Research 2019.
Quite a long list of references on nonextensive
statistical mechanics and its recent
successful
applications
can be found
here.
Here is a popular science article in the Science magazine (23 August 2002) on this approach.
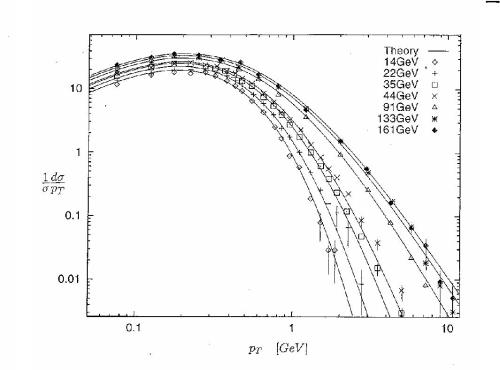
As an example, the following picture shows
differential cross sections of hadronic particles
as produced
in e+e- annihilation experiments.
The measurements were done by the
TASSO and
DELPHI collaboration.
Essentially
the figure shows how many particles with a given
transverse momentum p_T
are produced at a certain
center-of-mass energy E. The solid lines
are analytical predictions of a model based on nonextensive
statistical mechanics.
There is excellent agreement between
theory and experiments.
This can also be applied to cosmic rays, see recent paper of mine in
Scientific Reports (2018).

More details can be found in
C. Beck,
Non-extensive statistical mechanics and particle
spectra in elementary interactions,
Physica 286A , 164 (2000)
download ps file