Professor
Shahn Majid

Professor
Shahn Majid


Lay Persons Guide to My Research on
Quantum Spacetime
You could say that my
research is about absolutely nothing and completely
pointless. Both statements are correct, but let me
explain!!
First of all, my research
is mainly about empty space with absolutely nothing in
it. But Riemann in 1854 and Einstein in 1917 taught us
that empty space still has structure; it’s curved and
this curvature makes objects moving in it bend around,
and this bending was Einstein’s way to understand
gravity. Einstein also taught us that space and time
are really parts of a single 4-dimensional spacetime
continuum. So my research is about the structure of
space and time.
Now the thing is that
Einstein never really agreed with quantum mechanics,
whereas we now know since 1924 that on a subatomic
scale physics is `fuzzy’ due to quantum effects. This
fuzziness is expressed in the famous Heisenberg
uncertainty relations that you cannot perfectly
measure the position and momentum (roughly speaking,
velocity) of a particle at the same. My research takes
these ideas much further and says that due to quantum
effects you cannot measure the location in space and
time of an event to perfect accuracy; spacetime is
itself intrinsically fuzzy due to quantum
effects. That means that the mathematical
concept of a point in space and time does not apply;
the geometry of the real world does not truly have
points but rather has a quantum structure. That’s what
I work on more precisely, a new conception of
geometry.
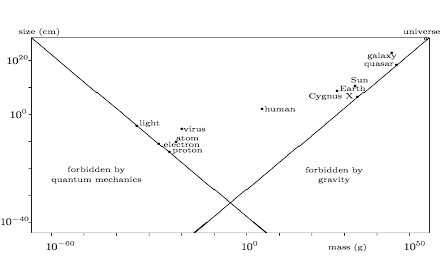
There are two clues in the
figure about where to go from here. The first is that
we, humans, are somewhat in the middle. I take that to
suggest that we built science around ourselves and in
the process we boxed ourselves in. In truth, Nature
does not know what mathematics, in particular, is in
our current maths books, so to truly break out of the
box we need to think about Pure Mathematics itself.
That’s how come I am a pure mathematician. The second
clue is a kind of symmetry or duality between the left
slope, elementary particles, and the right slope,
black holes. The search for the correct structure of
space and time led me since the 1980s to focus on a
kind of self-duality in the nature of mathematics.
You can read more online by exploring the menu at the top or my old Space and Time blog. You can read more in print in my book On Space and Time. You can read about my more mathematical work in algebra, geometry and category theory under the Research tab at the top.
Educated 1st degree Cambridge including part III in theoretical physics and PhD Harvard jointly in the mathematical physics and pure mathematics departments. After a year in Swansea, spent 10 years in the Department of Applied Mathematics and Theoretical Physics, Cambridge and as a Fellow of Pembroke College. Moved to Queen Mary in 1999, where I was Director of Pure Mathematics 2010-13. I have been an EPSRC Postdoctoral Fellow, an EPSRC Advanced Fellow, a Royal Society University Research Fellow and a Leverhulme Senior Research Fellow.
My Space and Time Blog