


Next: Numerical Data Types
Up: The External Representation of
Previous: Functions and Index Flags
Contents
Permutation groups
Permutation groups appear in many areas of design theory, in particular
as automorphism groups of designs.
The specification of an permutation group is:
permutation_group = element permutation_group {
attribute degree { xsd:positiveInteger } ,
attribute order { xsd:positiveInteger } ,
attribute domain { "points" },
generators ,
permutation_group_properties?
}
There are four compulsory properties:
- degree
An attribute giving the number 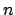 of points on which the permutations
are defined (the permutation group will then act on the indices
of points on which the permutations
are defined (the permutation group will then act on the indices
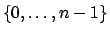 ).
).
- order
An attribute giving the number of permutations in the group.
- domain
- An attribute specifying the domain indexed by the points
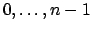 .
.
- generators
A list of permutations which generate the group. A permutation is
represented by the ordered list of its values (the images of the points
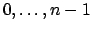 under the permutation).
under the permutation).
For example, the permutation group which is the automorphism group
of our Fano plane can be given as:
<permutation_group degree="7" domain="points" order="168">
<generators>
<permutation>
<z>1</z>
<z>0</z>
<z>2</z>
<z>3</z>
<z>5</z>
<z>4</z>
<z>6</z>
</permutation>
<permutation>
<z>0</z>
<z>2</z>
<z>1</z>
<z>3</z>
<z>4</z>
<z>6</z>
<z>5</z>
</permutation>
<permutation>
<z>0</z>
<z>3</z>
<z>4</z>
<z>1</z>
<z>2</z>
<z>5</z>
<z>6</z>
</permutation>
<permutation>
<z>0</z>
<z>1</z>
<z>2</z>
<z>5</z>
<z>6</z>
<z>3</z>
<z>4</z>
</permutation>
<permutation>
<z>0</z>
<z>1</z>
<z>2</z>
<z>4</z>
<z>3</z>
<z>6</z>
<z>5</z>
</permutation>
</generators>
</permutation_group>
There are also various properties which can optionally be specified:
- primitive
True if the group acts primitively on points. A permutation group is
primitive if it preserves no non-trivial equivalence relation.
By convention, we assume that a primitive group is transitive (that is,
any point can be carried to any other by some group element). (So the
trivial group acting on two points is not primitive.)
- generously_transitive, multiplicity_free,
stratifiable
Each orbit of the group acting on the set of ordered pairs of points can be
represented by a matrix of zeros and ones of order 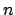 (which can be thought
of as the characteristic function of the orbit). These
basis matrices span the centraliser algebra of the
group (the algebra of all matrices commuting with the group elements).
Now the group is generously transitive if all the basis
matrices are symmetric; it is multiplicity-free if the basis
matrices commute; and it is stratifiable if the symmetrised
basis matrices commute. Each concept implies its successor in the order
given.
(which can be thought
of as the characteristic function of the orbit). These
basis matrices span the centraliser algebra of the
group (the algebra of all matrices commuting with the group elements).
Now the group is generously transitive if all the basis
matrices are symmetric; it is multiplicity-free if the basis
matrices commute; and it is stratifiable if the symmetrised
basis matrices commute. Each concept implies its successor in the order
given.
A transitive permutation group is generously transitive iff any two points
can be interchanged by some element of the group; it is multiplicity-free
iff no irreducible constituent of the permutation character occurs with
multiplicity greater than 1; and it is stratifiable iff the orbits of the
group on unordered pairs form an association scheme. All these properties
are false if the group is not transitive.
- no_orbits
The number of orbits on points. The group is transitive exactly when
there is just one orbit on points.
- degree_transitivity
The maximum number 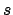 such that the group is
such that the group is 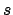 -transitive
on points (that is, any
-transitive
on points (that is, any 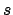 -tuple of distinct points can be carried
to any other by some group element).
-tuple of distinct points can be carried
to any other by some group element).
- rank
The number of orbits of the group on the set of ordered pairs of points.
Note that this is defined for any permutation group; if the group is
transitive, it is equal to the number of orbits of the stabiliser of a
point.
- cycle_type_representatives
see below
The cycle type of a permutation is the multiset of its cycle
lengths (when it is written as a product of disjoint cycles). The
element cycle_type_representative consists of
a cycle type and an element of the group having that cycle type, and
optionally the number of elements of the group having that cycle type.
cycle_type_representatives is a list
of these cycle_type_representative elements,
one for each cycle type represented by an element of the group.
For the example above, there are five cycle types,
![$[7], [1,2,4], [1,3,3],
[1,1,1,2,2]$](img39.png) , and
, and
![$[1,1,1,1,1,1,1]$](img40.png) (the last being the identity). The
cycle type representative for the second type is:
(the last being the identity). The
cycle type representative for the second type is:
<cycle_type_representative>
<permutation>
<z>0</z>
<z>2</z>
<z>1</z>
<z>5</z>
<z>6</z>
<z>4</z>
<z>3</z>
</permutation>
<cycle_type ordered="true"><z>1</z><z>2</z><z>4</z></cycle_type>
<no_having_cycle_type>
<z>42</z>
</no_having_cycle_type>
</cycle_type_representative>



Next: Numerical Data Types
Up: The External Representation of
Previous: Functions and Index Flags
Contents
Peter Dobcsanyi
2003-12-15
![]() of points on which the permutations
are defined (the permutation group will then act on the indices
of points on which the permutations
are defined (the permutation group will then act on the indices
![]() ).
).
![]() under the permutation).
under the permutation).