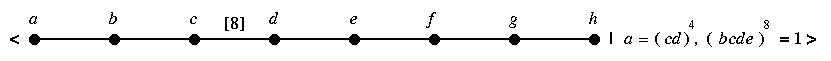Sporadic Suzuki group Suz

Order = 448 345 497 600 = 2¹³.3⁷.5².7.11.13.
Mult = 6.
Out = 2.

Robert Wilson's ATLAS page for the Suzuki group Suz is available here.

Suz: Length ??, 2-generator, ?-relator.

3.Suz:2: Length 177, 8-generator, 37-relator.

I haven't found any way to make this `picture' look good. I will be glad to hear from anyone with any good ideas about this.

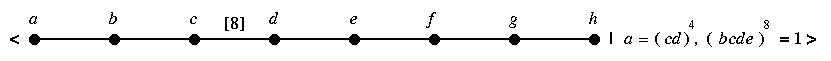
Remark: LHS-presentation. The calculations of length and number of relators in the above (Coxeter) presentation exclude the obviously redundant (cd)⁸ = 1. The presentation is available in MAGMA format here and we have included the subgroups below too. Some of the subgroups below have too large index for coset enumeration, many are not maximal and not all of the subgroups give rise to faithful permutation representations.

Some subgroups.

Suzuki chain.

M1 = < a, b, c, d, e, f, g > = G₂(4):2 of order 503 193 600 and index 5 346 = 1 782 x 3.
M2 = < a, b, c, d, e, f > = J₂:2 of order 1 209 600 and index 2 223 936.
M3 = < a, b, c, d, e > = U₃(3):2 = G₂(2) of order 12 096 and index 222 393 600.
M4 = < a, b, c, d > = PGL₂(7) = L₃(2):2 of order 336 and index 8 006 169 600.
M5 = < a, b, c > = S₄ of order 24 and index 112 086 374 400.
M6 = < a, b > = S₃ of order 6 and index 448 345 497 600.

Other subgroups.

None for now.

Last updated 29^th June, 1997

John N. Bray